Both historically and in the contemporary environment, recorded noise presents many problems. To a large degree this has been combatted with the use of noise gating. Whilst this works well it has limitations in that a quite large signal to noise ratio is required to obtain transparent gating without obvious breathing artifacts. This is particularly true in the case of music content which remains quite high in overall level but is confined to a limited band of frequencies such that a considerable amount of noise is not masked by the instrument.
A typical example might be bass guitar or piano playing in a low register where the noise at high frequencies are readily apparently because it is not being masked by the instrument. In such circumstances a conventional gate is useless and more disturbingly, if gating was being used and the instrument just cut in making the gate turn off, suddenly we hear a sizeable quantity of noise that isn’t being masked by the instrument. If we could break the signal into bands and gate each band independently then the high frequency bands in this case would only cut in when there is sufficient music content to mask the noise so that noise in the former case would not be heard in a multiband gate implementation.
To some extent, in a multitrack context this stated issue can be compensated for by bandlimiting the instrument to its spectrum range but this is problematic for an instrument which can span the entire range but might be in a restricted range at one point and not at another at a different point in time. Suffice to say, multiband gating handles this simply and transparently, the only exception being when the baseline signal to noise ratio is so poor that the music (when present) does not completely mask the noise. In a mastering context where instruments are combined into common channels conventional gate becomes more problematic and multiband gating more relevant.
The key aspect to multiband gating is the resolution of filtering (how many bands) and how the gating is handled to minimise the likelihood of audibly disturbing artifacts. On the issue of resolution, Har-Bal Multiband Gate uses sufficient gate bands to cover most of the audible spectrum with a 1/3 octave resolution. For frequencies below around 500Hz the bands become considerably wider. The reason for this is twofold: (1) at lower frequencies the critical bandwidth of human hearing increases quite substantially (and is why intervals of a third can sound dissonant in a low register but consonant in a higher one) and, (2) by following this approach the filtering can efficiently be implemented with a relatively short finite impulse response filter thereby making the processing CPU efficient.
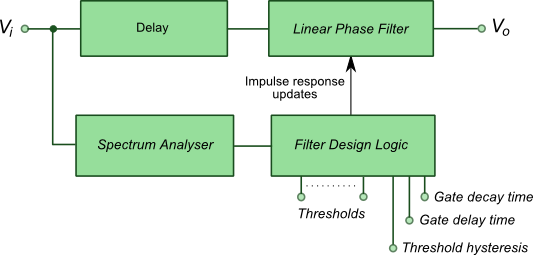
The processing chain used within Har-Bal Multiband Gate is shown below. The input signal is fed into a spectrum analyser implemented using the same resolution Fourier Transform as the resolution of the finite impulse response filter that realises the gate. Because the transitioning of filter responses takes a finite amount of time (half the impulse response length), the filter realising the gate is time delayed relative to what the analyser sees so that the gate frequency response changes early enough to pick up the opening of any music content when the gate opens. The filter design logic takes inputs from the spectrum analyser and the thresholds, hysteresis, gate delay and gate decay times to design the frequency response of the gate filter.
Block Diagram of the Processing Chain in Har-Bal Multiband Gate
One common approach to time varying filtering using Fourier Transforms involves a so called filter bank approach. Whilst this can be computationally advantageous it can also result in aliasing artifacts in the processing of band content. The approach taken hear is classical Finite Impulse Response linear phase filtering with windowing used to transition from one response to the next so no aliasing distortion is possible. That combined with the way in which the gating is controlled through delay, decay and hysteresis affords the ability to do effective gating with little or no obvious artifact.
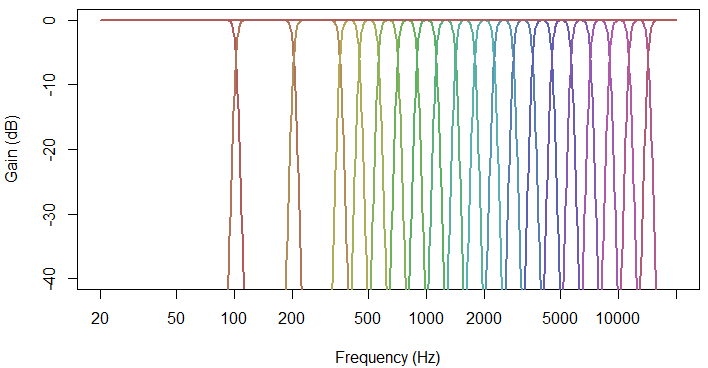
The band frequency responses and their sum is illustrated below. The first three bands are course in resolution because low frequency critical bandwidth is wide at low frequencies. The bandwidths are also deliberately course to allow small FIR filter size to realise the frequency response and that small size consequently lowers the CPU demand to implement the signal processing. Note that all bands summed together give a flat frequency response and because the filter realisation is a linear phase one there is no phase distortion, even in the case of a number of bands having non-unity gain.
Band Frequency Responses and Combined Response
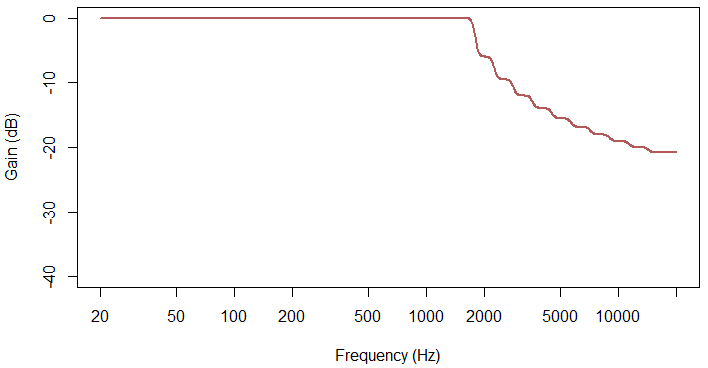
The shape of the filter frequency response is controlled by the Filter Design Logic. By using trigger and decay logic to all a gain term to each band depending on whether the gate is active or not, a band based noise gating response can be realised through a time varying frequency response. As an illustration the figure below shows the frequency response realised by applying gains inversely proportional to frequency for bands above 1.8kHz.
