A Time to Design A New Loudspeaker System
It’s been a long time since I last designed and built a loudspeaker system. The year of 1992 In fact and as much as I have enjoyed and do enjoy them still, I have reached a point of curious temptation. A temptation to see if I can produce a new system with hopefully better performance and a performance better suited to the advancing years of my hearing.
Whilst my existing speakers perform well they have always had one shortcoming and that is a weakness of output above 10kHz, which whilst giving a charming analog sound for youthful ears has increasingly become a noticeable limitation for my mid life ones. If for no other reason than that, I am tempted to construct a system more capable in that area. That and a curiosity as to how much better drivers may now be given 15 years of evolution.
Since the days of my last design I’ve harboured a desire to publish what I knew on the subject but never managed to do so. This latest desire provides the vehicle for such a foray. So in the coming weeks and months, and given my procrastinations, perhaps years, I shall attempt to shed light on the process of designing an affordable and good sounding loudspeaker system.
What makes for a Good Loudspeaker System?
Is it on-axis frequency response? Is it low distortion? Is it linear phase response? Is it polar response? Of those characteristics the ones most often coveted in product specifications and technical reviews are on-axis frequency response and distortion, whilst linear phase response takes on an esoteric magical status amongst hi-end speakers. Whilst those coveted characteristics are important I generally feel they are overstated.
The true quality comes from a combination of factors including some of those mentioned but the one attribute that dominates in my thinking is uniformity of frequency response, not just confined to the on-axis case, but also how it changes off axis in both the vertical and horizontal plane. Why should that be? The simple fact of that matter is that what we actually hear in a normal listening environment is strongly influenced by the ambient field (the sound reverberating in this listening room), with only perhaps 1/3 of the sound pressure coming from direct line of sight radiation from the driver. If you find this hard to believe and you have a back yard, put a loudspeaker out in the yard and play something back. Apart from the lack of life in the rendition of sound, you will also hear a substantial drop in volume of the sound because the ambient field is largely not there. In a room the speaker sounds so much louder because what you are hearing is dominated by the reverberant field.
What we hear is largely reflected sound, not just the direct path from the loudspeaker to our ears.
Well, so what you might say! How does this imply an importance of uniformity in polar response? It is crucial because the reverberant field is made of the radiated sound emanating from the loudspeaker in all directions, not just the line of sight from loudspeaker to you. In mathematical terms it is the sum (or integral) of the power radiated around a sphere enclosing the driver. As such, the colour of the sound we hear is determined by the colour the frequency response of the loudspeaker system in all directions, not just the one! As such, it is perfectly feasible to have a loudspeaker that has a brilliant on axis frequency response but when put in a real room sounds deficient because the off axis response has big anomalies. A simple example might be the difference in sound quality between a full range driver and a two way loudspeaker system. Because the full range driver has a lower dispersion at high frequencies if sounds duller than the tweeter / woofer combination, despite them both having a nominally flat on axis response.
So if a well behaved polar response is the ideal why not go for electrostatic loudspeakers? What is the ideal polar response and is there an ideal response? In truth there may well not be one, only a compromise. Why should this be so? What we are trying to achieve in any loudspeaker system is the faithful reproduction of a collection of instruments such that we feel as if the instruments are in the room with us, or we’re in the hall with them. For this to sound true it requires that the loudspeaker has a similar polar response to the instruments we are attempting to reproduce, otherwise the colour of the reproduced sound will be altered in any real room. At this point it should then be obvious that we cannot have a similar polar response for all instruments as they will all have different characteristics.
The ideal is then the compromise of choosing a polar response similar to most instruments but clearly not all. Fortunately the polar response from a typical dome tweeter is pretty compatible with most instruments. Perhaps the ones where it falls down on is the striking of cymbals, which typically will have an omnidirectional response (at least in one plane). As such, cymbals reproduced through dynamic loudspeaker systems never sound as bright as they do in real life but reproduced through electrostatic speakers they do (perhaps explaining the attractiveness of them in some peoples opinion). However, whilst cymbals will sound right on electrostatics the down side is that virtually everything else will sound too bright to be real, though I think many people like that exaggerated brightness.
The other benefit of having the restricted polar response of dynamic loudspeakers is having an easier time coping with plane reflections off walls. The bane of good sound reproduction is having false images of the loudspeakers through reflections off walls, the solution of which is strategically placed diffusers to scatter the reflection. With dynamic loudspeakers we generally only have big troubles with side and rear wall reflections whereas for electrostatics we’ll also have problematic reflections off the wall in front of the listening position, so that will mean extra requirements for room treatment and extra costs.
Factors Governing Loudspeaker System Polar Response
So what are the principle factors governing whether we have a uniform polar response? Driver quality obviously plays an important part and is the reason why dynamic loudspeaker systems usually have different sets of drivers covering different parts of the spectrum (woofers, tweeters etc) rather than full range drivers. The other major factor is the nature of the crossover and the choice of crossover frequencies. In the latter, the crossover frequency should be chosen such that the off axis frequency response does not develop mid-range weakness. This generally happens if the lower frequency driver is made to take control of more of the spectrum than it can deliver off axis. For two way systems this is typical of speakers that have a crossover point of around 3kHz-5kHz or higher because most woofers, even small ones, start to become pretty directional at around 2kHz and this leads to an off axis frequency response that is weak between 2kHz and the crossover point.
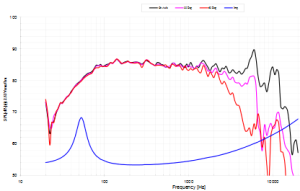
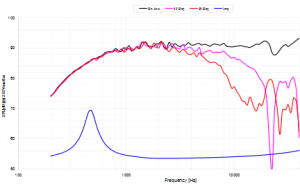
For example, below we see manufacturers response tests for a typical woofer-midrange unit and and tweeter unit. If we happened to use those in combination with a 3kHz crossover point then the 60 degree off axis response of the woofer-mid unit is 8dB down whereas the tweeter is only about 1.5dB down. It is clear then that crossing at 3kHz will give an off axis hole in the response. On the other hand, if we set the crossover point at 2kHz the woofer-mid unit off axis response is only about 2.5dB down and the tweeter off axis response is essentially not down at all, so we have an off axis hole but it is significantly smaller than when crossed at 3kHz.
Typical woofer-mid response (Pearless 830656). There is a dramatic drop in off axis output above 2kHz.
Typical tweeter response (Vifa XT25TG30-04). It starts becoming increasingly directional at around 8kHz but is essentially omni-drectional at 2kHz.
In short, it is best to have the tweeter cover as much of the audible spectrum as is practically possible but how much is possible will depend upon the choice of the tweeter and the crossover cutoff slope. You can see that the tweeter response remains strong down to 1kHz, so maybe we could cross it that low and have a seamless polar response. The factor limiting this choice is the power handling of the tweeter which can typically dissipate around 5W of electrical energy in the voice coil. The lower the crossover frequency the more power gets sent to the tweeter (music is typically has a tapered pink noise spectrum) thus reducing the system power handling of the loudspeaker system. For reasons of practicality, a crossover point between 1.5 and 2kHz is what we are typically restricted to.
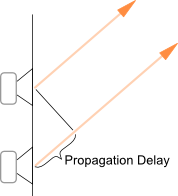
There still remains one other point to consider. We have assumed that we can simply join the two driver responses together and obtain a fair representation of how they will perform. Lets say we mount the drivers in a vertical array. For this configuration that approximation will be about right for the horizontal plane but not for the vertical plane. The drivers are not coherent. The sound radiation centres are not coincident but are physically separated, so as we move off axis the phase relationship between the two drivers changes by virtue of the propagation delay.
Propagation delay resulting from two drivers when off axis in the vertical plane.
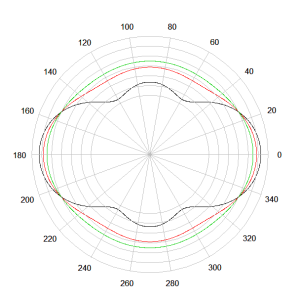
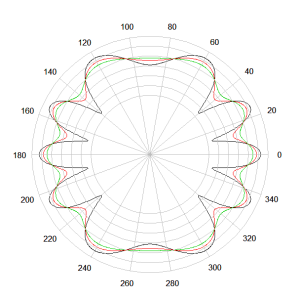
That propagation delay will give rise to an interference pattern, the strength of which will be influenced by the steepness of the crossover. To illustrate, consider the idealised case of two point sources 20cm apart and crossed over at 2kHz with 1st, 2nd and 3rd order Butterworth response high and low pass filters. The resulting vertical plane polar response at 1kHz (1 octave below crossover) and 4kHz (1 octave above crossover) is shown below. It is clear from these two polar plots that the filter order / cutoff slope of the crossover has a dramatic effect on the off axis performance near the crossover frequency.
Comparison of Vertical Polar Response of Two Idealised Point Sources 20cm Apart at 1kHz with a Crossover Frequency of 2kHz : Black = 1st Order Crossover, Red = 2nd Order Crossover and Green = 3rd Order Crossover.
For the 1st order crossover (6dB attenuation per octave cutoff slope) the polar response varies in magnitude by as much as 10dB, the 2nd order crossover (12dB attenuation per octave cutoff slope) varies by 4dB and the 3rd order crossover (18dB attenuation per octave cutoff slope) varies by 2dB. The trend is clear. The higher the cutoff slope of the crossover the less spectrum overlap of the drivers and consequently the less interference between the drivers when moving off (vertical axis).
Comparison of Vertical Polar Response of Two Idealised Point Sources 20cm Apart at 4kHz with a Crossover Frequency of 2kHz : Black = 1st Order Crossover, Red = 2nd Order Crossover and Green = 3rd Order Crossover.
At this point it is worthwhile asking the question “is aiming for a linear phase response a worthwhile goal in a passive loudspeaker system”? This question arises since a 1st order crossover is a requirement to obtaining a linear phase response with an analog crossover : any other filter order cannot realise a linear phase response! The goal of linear phase therefore comes at a substantial cost of having a pretty ordinary polar response in the vertical plane. This is further compounded by the general requirement of a higher crossover frequency to enable reasonable power handling for the tweeter, which usually means that linear phase speakers are typically 4 way crossovers with four sets of drivers (more if they are in a paired configuration). That means three crossover points to have compromised polar response (in the vertical plane) over a substantial bandwidth (two octaves).
Because of these factors and the snowballing costs involved, my view remains that passive crossover linear phase speaker systems are simply not worthwhile and will not result in a very pleasing sound in typical listening environments. That is not to say that it isn’t possible to solve this dilemma. It is, but to solve it requires an active crossover with digital linear phase filtering and I’m not proposing to design an active digital system but a passive analog one.
Is there a substantial cost associated with a non-linear phase response? In my view, no. I don’t dispute that non-linear phase response can lead to a different quality of sound, that is inevitable, but the design choices you are forced to make with a linear phase design introduces so much non-uniformity in the vertical polar response that the colouration of the ambient sound field is going to be much more than the negative effect of a phase discontinuity around the crossover point.
Conclusions
In summary, a good loudspeaker system can be constructed by choosing good quality drivers with well behaved on and off axis response and combining them by choosing crossover points which result in the least non-uniformity in the off axis response. Ideally, the tweeter should carry as much bandwidth as is practically possible. We also need to choose a crossover order that is high enough to confine the vertical polar response anomalies to a narrow band of frequencies around the crossover point. This generally means at least a third order crossover.
to be continued…